2.2.3. Síťové grafy
Síťový graf je matematickým modelem projektu, který přesně popisuje závislosti jednotlivých činností. Jde o orientovaný graf, který se skládá z uzlů a hran.
Sestavování síťových grafů není složitou záležitostí, je však třeba respektovat některá jednoduchá pravidla:
- síťový graf musí mít právě jeden výchozí a právě jeden koncový uzel;
- každému uzlu s výjimkou výchozího musí předcházet alespoň jedna hrana;
- po každém uzlu s výjimkou koncového musí následovat alespoň jedna hrana;
- libovolné dva uzly v grafu může spojovat pouze jedna hrana.
Podle interpretace základních prvků síťového grafu rozlišujeme dva druhy těchto grafů: hranově nebo uzlově definované síťové grafy.
Hranově definované síťové grafy jsou modely, kde hrany grafu reprezentují činnosti projektu. uzly grafu pak představují události. Přitom událostí rozumíme začátky a konce jednotlivých činností.

Zdroj: Fiala (2004)
Uzlově definované síťové grafy jsou modely, kde uzly grafu reprezentují jednotlivé činnosti v rámci projektu, zatímco hrany vyjadřují vazby mezi těmito činnostmi.

Zdroj: Fiala (2004)
V dalším výkladu se zaměříme pouze na konstrukci hranově definovaných síťových grafů.
Každý síťový graf musí správně popisovat závislosti a návaznosti jednotlivých činností v rámci projektu. Technologické nebo organizační vazby vyjádříme tím, že koncový uzel předcházející činnosti bude zároveň počátečním uzlem činností následujících (viz obrázek);

Zdroj: Fiala (2004)
Při větším počtu činností může obrázek vypadat takto:

Zdroj: Fiala (2004)
V některých případech je třeba použít tzv. fiktivních činností. Fiktivní činnost ve skutečnosti neprobíhá (má nulovou časovou délku). Jejich použití je v hranově definovaném grafu nutné pro správné vyjádření některých závislostí. Použití fiktivních činností zajistí, že budou respektována výše uvedená pravidla pro tvorbu síťových grafů. Síťový graf tak bude orientovaným grafem, který má právě jeden jasně definovaný začátek a konec. Fiktivní činnosti použijeme zejména v těchto případech:
- k oddělení závislých činností od nezávislých;
Obr. 9 - Použití fiktivních činností – oddělení závislých činností od nezávislých

Zdroj: Fiala (2004)
- k oddělení souběžných fiktivních činností
Obr. 10 - Použití fiktivních činností – oddělení souběžných činností

Zdroj: Fiala (2004)
- k zajištění toho, aby měl síťový graf jeden začátek;
Obr. 11 - Použití fiktivních činností – zajištění aby měl graf právě jeden začátek

Zdroj: Fiala (2004)
- k zajištění toho, aby měl síťový graf jeden konec;
Obr. 12 - Použití fiktivních činností – zajištění aby měl graf právě jeden konec

Zdroj: Fiala (2004)
- jestliže je návaznost prací směrována před termín dokončení předchozí činnosti.
Obr. 13 - Použití fiktivních činností – jestliže je návaznost prací směrována před termín dokončení předchozí činnosti

Zdroj: Fiala (2004)
Takto sestavený síťový graf může být náležitě ohodnocen, tj. doplněn o žádoucí číselné údaje. Ohodnocení hran grafu tak může představovat údaje o čase, nákladech nebo zdrojích pro jednotlivé činnosti.
Obr. 14 - Příklad ohodnoceného síťového grafuDále
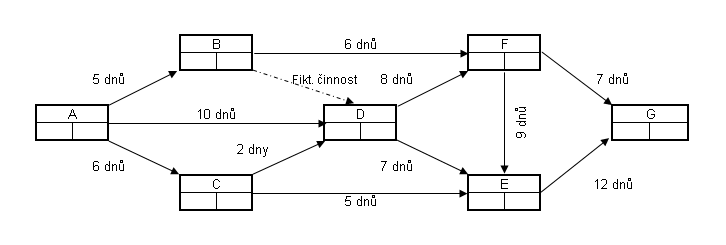
Zdroj: Fiala (2004)
- k zajištění toho, aby měl síťový graf jeden konec;


